前置知识
1、跨导 gm 的表达
$$ \begin{align*} g_m&=\mu C_{ox}\frac{W}{L}(V_{GS}- V_{TH}) \\ &=\sqrt[]{2\mu C_{ox}\frac{W}{L}I_D} \\ &=\frac{2I_D}{(V_{GS}- V_{TH})} \end{align*} $$2、放大器的小信号电压增益
$$ A_V=G_m\times R_{out} $$其中，Gm 为输出短路到地计算的跨导、Rout 为输入短路到地计算的输出阻抗。
3、二极管型连接器件的阻抗
二极管型连接器件从漏端看去的小信号阻抗为：
$$ r=\frac{1}{g_m} $$4、带源极负反馈的共源极
对于带源极负反馈的共源极，其跨导为：
$$ G_m=\frac{g_{m1}}{1+g_{m1}R_s} $$该电路具有反相作用，因此其小信号电压增益为：
$$ \begin{align*} A_V&=-G_mR_D\\ &=-\frac{g_{m1}R_D}{1+g_{m1}R_s} \end{align*} $$环路分析
由于 M2 的 Vgs < M1 的 Vgs，因此通常有：
$$ (W/L)_{M2}:(W/L)_{M1}=K:1 $$通常，我们认为左边的环路连接方式稳定，为什么呢？这就需要对环路进行分析。
1、定性分析
对于左边的环路连接方式，从 M3 的栅极断开环路，令 M3 栅压上升时，M3 为维持电流恒定而分压增加，导致 M1、M2 栅压下降，M2 为维持电流恒定分压增加，导致 （M3、）M4 栅压上升，正反馈；
类似地，对于右边的环路连接方式，从 M4 栅极断开环路，令 M4 栅压上升时，M4 为维持电流恒定而吃掉更多电压，M1、M2 栅压降低，M1 为维持电流恒定吃掉更多电压，从而导致 M3（、M4） 栅压上升，正反馈。
2、定量分析
接下来，分别计算两种环路的环路增益。
2.1 左边的环路连接方式
在 M3 的栅极断开环路，施加小信号电压 Vx，M3 与 M1 形成了一个以二极管连接形式的 M1 为负载的共源极放大器，则该部分的小信号增益为：
$$ \begin{align*} A_{V1}&=-G_mR_{out}\\ &=-g_{m3}\times\frac{1}{g_{m1}} \end{align*} $$M2 与 M4 构成了带有源极负反馈的共源极，小信号增益为：
$$ \begin{align*} A_{V2}&=-G_mR_{out}\\ &=-\frac{g_{m2}\times \frac{1}{g_{m4}}}{1+g_{m2}R_S} \end{align*} $$整个环路的增益为：
$$ \begin{align*} LG&=A_{V1}A_{V2}\\ &=\frac{g_{m3}}{g_{m1}}\frac{g_{m2}\times \frac{1}{g_{m4}}}{1+g_{m2}R_S}\mid_{g_{m3}=g_{m4}}\\ &=\frac{1}{\frac{g_{m1}}{g_{m2}}(1+g_{m2}R_S)} \end{align*} $$由 gm 的表达式可得：
$$ \left\{\begin{matrix} g_{m1}=\sqrt[]{2\mu C_{ox}(\frac{W}{L})_1I_D}\\ g_{m2}=\sqrt[]{2\mu C_{ox}K(\frac{W}{L})_1I_D} \end{matrix} \right. \Rightarrow \frac{g_{m1}}{g_{m2}}=\frac{1}{\sqrt{K}} $$通常，我们取 K=4，gm2×Rs>1，则分母大于 1，环路增益小于 1，环路稳定。
2.2 右边的环路连接方式
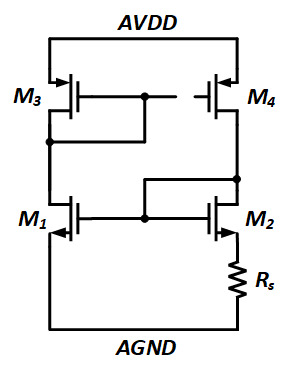
与之前的分析类似，M4 与 M2 形成共源极，增益为：
$$ \begin{align*} A_{V1}&=-G_mR_{out}\\ &=-g_{m4}\times(\frac{1}{g_{m2}}+R_S) \end{align*} $$M1 与 M3 形成共源极，增益为：
$$ \begin{align*} A_{V2}&=-G_mR_{out}\\ &=-g_{m1}\times(\frac{1}{g_{m3}}) \end{align*} $$环路增益为：
$$ \begin{align*} LG&=A_{V1}A_{V2}\\ &=g_{m1}g_{m4}\frac{1}{g_{m3}}(\frac{1}{g_{m2}}+R_S)\mid_{g_{m3}=g_{m4}}\\ &=(\frac{1}{\frac{g_{m1}}{g_{m2}}(1+g_{m2}R_S)})^{-1} \end{align*} $$此环路的增益为之前计算环路增益的倒数，由于之前计算的环路增益 < 1；因此该环路增益 > 1；环路不稳定。