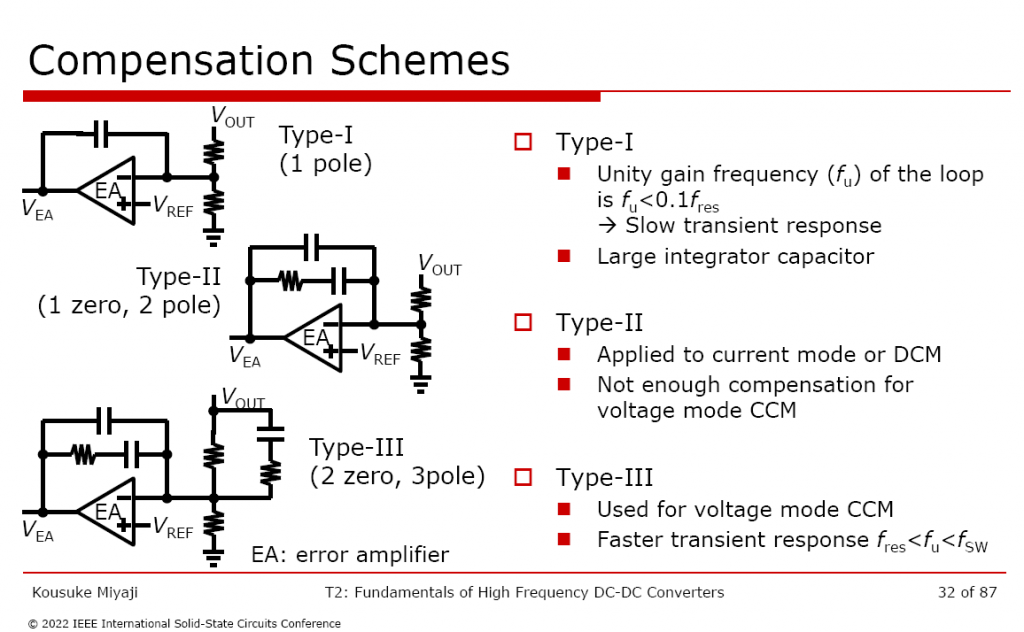
基于运放的 Type-I、Type-II、Type-III 补偿器传递函数推导 2024年10月15日
IC Design & EDA

Type-I Compensator

I 型补偿具有一个极点，运用运算放大器的虚短虚断特性，其传递函数推导如下：

$$ \frac{V_e-V_-}{\frac{1}{sC_1}} = \frac{V_- -V_o}{R_1} $$

对 AC 小信号分析，Vx 为小信号地，则有：

$$ \frac{V_e}{V_o} = -\frac{1}{sC_1R_1} $$

该传递函数具有一个极点：

$$ p_0=0 $$

Type-II Compensator

II 型补偿器可以最高提供 90° 的相位提升（通常在 50° 左右），常用于电流模控制的 DC-DC 环路或是 DCM 模式下的电压模 DC-DC 环路补偿。

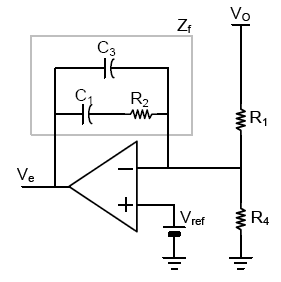
令 C1、C3、R2 组成的电路部分为 Zf，与 Type-I 的分析类似，我们有：

$$ \frac{V_e-V_-}{Z_f} = \frac{V_- -V_o}{R_1}\\ \begin{align} Z_f&=\frac{1}{sC_3}//(\frac{1}{sC_1}+R_2 )\\ &=\frac{\frac{1}{sC_3}(\frac{1}{sC_1}+R_2 ) }{\frac{1}{sC_3}+\frac{1}{sC_1}+R_2} \\ &=\frac{1+sC_1R_2}{s^2C_1C_3R_2+s(C_1+C_3)} \end{align} $$

对 AC 小信号分析，Vx 为小信号地，则有：

$$ \begin{align} \frac{V_e}{V_o} &= -\frac{1+sC_1R_2}{s^2C_1C_3R_1R_2+sR_1(C_1+C_3)}\\ &=-\frac{1+sC_1R_2}{sR_1(C_1+C_3)(1+sR_2(C_1//C_3))} \end{align} $$

通常，我们取 C1>>C3，则：

$$ \frac{V_e}{V_o} \approx -\frac{1+sC_1R_2}{sR_1C_1(1+sR_2C_3)} $$

该传递函数具有两个极点，一个零点：

$$ \begin{align} p_0&=0\\ p_1&=-\frac{1}{R_2C_3} \\ z_1&=-\frac{1}{R_2C_1} \end{align} $$

Type-III Compensator

III 型补偿器可以最高提供 180° 的相位提升（通常在 130° 左右），常用于电压模 DC-DC 环路补偿。

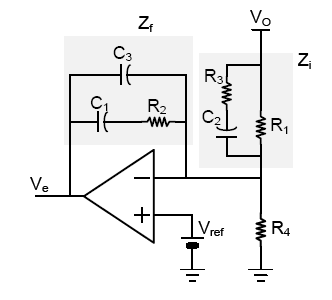
令 C1、C3、R2 组成的电路部分为 Zf，R1、R3、C2 组成的电路部分为 Zi，与 Type-II 的分析类似，我们有：

$$ \frac{V_e-V_-}{Z_f} = \frac{V_- -V_o}{Z_i}\\ \begin{align} Z_f&=\frac{1}{sC_3}//(\frac{1}{sC_1}+R_2 )\\ &=\frac{\frac{1}{sC_3}(\frac{1}{sC_1}+R_2 ) }{\frac{1}{sC_3}+\frac{1}{sC_1}+R_2} \\ &=\frac{1+sC_1R_2}{s^2C_1C_3R_2+s(C_1+C_3)} \\ Z_i&=R_1//(\frac{1}{sC_2}+R_3 )\\ &=\frac{R_1(\frac{1}{sC_2}+R_3 ) }{R_1+\frac{1}{sC_2}+R_3} \\ &=\frac{R_1+sC_2R_1R_3}{1+sC_2(R_1+R_3)} \\ \end{align} $$

对 AC 小信号分析，Vx 为小信号地，则有：

$$ \frac{V_e}{V_o} = -\frac{(1+sC_2(R_1+R_3))(1+sC_1R_2)}{(sR_1(C_1+C_3))(1+sC_2R_3)(1+s\frac{C_1C_3R_2}{C_1+C_3} )} $$

通常，我们取 C1>>C3，则：

$$ \frac{V_e}{V_o} \approx -\frac{(1+sC_2(R_1+R_3))(1+sC_1R_2)}{(sR_1C_1)(1+sC_2R_3)(1+sR_2C_3 )} $$

该传递函数具有三个极点，两个零点：

$$ \begin{align} p_0&=0\\ p_1&=-\frac{1}{R_3C_2} \\ p_2&=-\frac{1}{R_2C_3} \\ z_1&=-\frac{1}{R_2C_1} \\ z_1&=-\frac{1}{(R_1+R_3)C_2} \\ \end{align} $$

参考文献：Demystifying Type II and Type III Compensators Using OpAmp and OTA for DCDC Converters – Texas Instruments

Demystifying Type II and Type III Compensators Using OpAmp and OTA for DCDC Converters下载