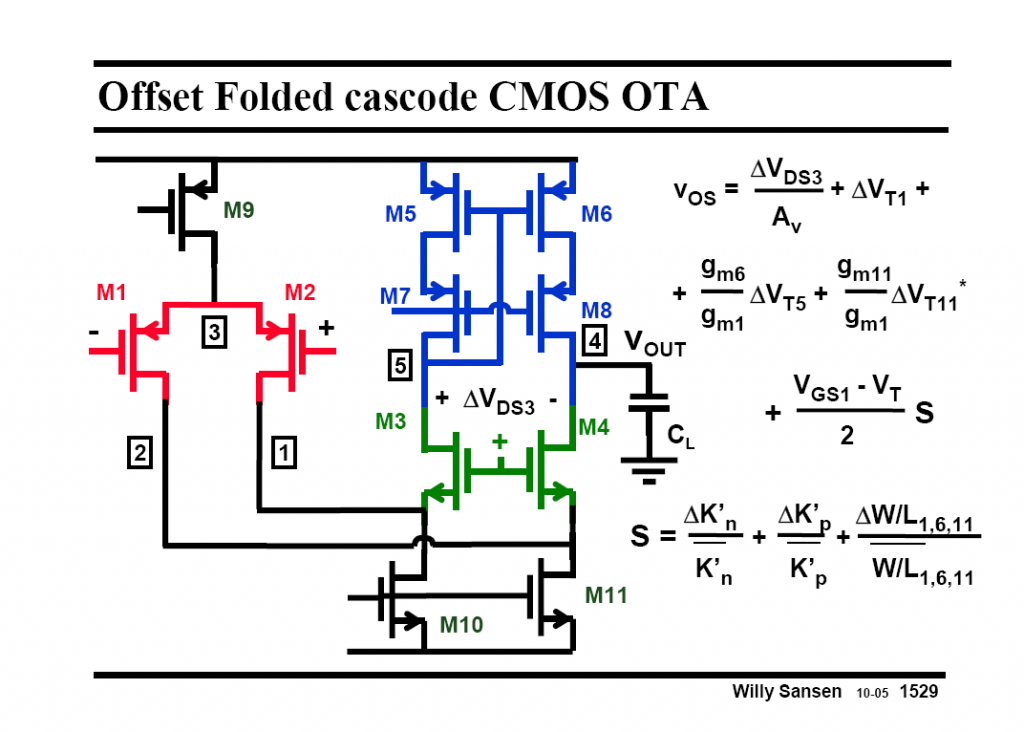
---

引入

在实际电路中，由于非理想因素的存在会导致器件之间产生物理上的 Mismatch，进而导致了电路 Offset 的存在。通常，我们可以通过 Monte Carlo 仿真来对这一情况进行评估仿真。

忽略沟道长度调制效应，晶体管在饱和区的电流可以表示为：

$$ \begin{align} I_D & = \frac{1}{2} \mu C_{ox}\frac{W}{L}(V_{GS}-V_{TH}) ^2\\ & = \frac{1}{2} \beta (V_{GS}-V_{TH}) ^2，其中 \beta =\mu C_{ox}\frac{W}{L} \end{align} $$

通过上式，在 V_GS 恒定的情况下，我们可以将失配大体分为 β 失配与 V_TH 失配。

在上图所示的折叠式共源共栅运算放大器中，M1-2、M5-6 以及 M10-11 产生的失配对 Offset 的贡献度最显著，而 M3-4、M7-8 产生的失配对 Offset 的贡献度较不明显（类比噪声的贡献度）。因此，在计算中我们不考虑 M3-4、M7-8 产生的失配。

下文计算以 M5-6 为例，假定 C_ox 为恒定值，失配量 Δ 极小，且计算一个项目的失配时假定其他项目不存在失配。I_D5,6=I_D1,2=I_D=1/2I_D10,11。

---

失配电流的推导

β 失配导致的 ΔI (β)

$$由于 \beta =\mu C_{ox}\frac{W}{L}，我们分别推导 \mu，W，L 失配的表达式，进而得到 \beta 失配的表达。$$

对于 μ 失配，有：

$$ \begin{align} I_{D5}&=\frac{1}{2}\mu _5C_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2 \\ I_{D6}&=\frac{1}{2}\mu _6C_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2 \\ \newline \Delta I_D (\mu)&=I_{D5}-I_{D6} \\ &=\frac{1}{2}(\mu _5-\mu _6)C_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2\\ &=\frac{1}{2}\Delta \mu C_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2 \\ &=\frac{1}{2}\Delta \mu \frac{\mu }{\mu } C_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2 \\ &=\frac{1}{2}\mu C_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2 \frac{\Delta \mu }{\mu }\\ &=I_D \frac{\Delta \mu }{\mu }\\ \end{align} $$

同理，对于 W 失配，有：

$$ \Delta I_D(W)=I_D \frac{\Delta W }{W } $$

对于 L 失配，有：

$$ \begin{align} I_{D5}&=\frac{1}{2}\mu C_{ox}\frac{W}{L_5}(V_{GS}-V_{TH})^2 \\ I_{D6}&=\frac{1}{2}\mu C_{ox}\frac{W}{L_6}(V_{GS}-V_{TH})^2 \\ L_6 &= L_5+\Delta L\\ \newline \Delta I_D(L)&=I_{D5}-I_{D6} \\ &=\frac{1}{2}\mu C_{ox}(\frac{W}{L_5}-\frac{W}{L_6})(V_{GS}-V_{TH})^2\\ &=\frac{1}{2}\mu C_{ox}(\frac{W}{L_5}-\frac{W}{L_5+\Delta L})(V_{GS}-V_{TH})^2\\ &=\frac{1}{2}\mu C_{ox}\frac{W}{L}(\frac{\Delta L}{L+\Delta L})(V_{GS}-V_{TH})^2\\ &=I_D\frac{\Delta L}{L+\Delta L}\\ \newline 又因为 \Delta L &\rightarrow 0，有：\\ \Delta I_D(L)&=I_D\frac{\Delta L}{L+\Delta L} \\ & \approx I_D\frac{\Delta L}{L} \end{align} $$

对上述结果进行归纳总结，我们可以得到 β 失配导致的 ΔI (β) 的表达式为：

$$ \Delta I(\beta )=I_D\frac{\Delta \beta }{\beta } $$

V_TH 失配导致的 ΔI (V_TH)

\begin{align} I_{D5}&=\frac{1}{2}\mu C_{ox}\frac{W}{L}(V_{GS}-V_{TH5})^2 \\ I_{D6}&=\frac{1}{2}\mu C_{ox}\frac{W}{L}(V_{GS}-V_{TH6})^2 \\ V_{TH6} &= V_{TH5}+\Delta V_{TH}\\ \newline \Delta I_D(V_{TH})&=I_{D5}-I_{D6} \\ &=\frac{1}{2}\mu C_{ox}\frac{W}{L}[(V_{GS}-V_{TH5})^2-(V_{GS}-V_{TH6})^2 ]\\ &=\frac{1}{2}\mu C_{ox}\frac{W}{L}[2\Delta V_{TH}(V_{GS}-V_{TH})-\Delta V_{TH}^2]\\ \newline 又因为 \Delta V_{TH} &\rightarrow 0，g_m=\mu C_{ox}\frac{W}{L}(V_{GS}-V_{TH})：\\ \Delta I_D(V_{TH})&\approx\mu C_{ox}\frac{W}{L}(V_{GS}-V_{TH})\Delta V_{TH}\\ &=g_m\Delta V_{TH} \end{align}

---

输入端等效 V_OS 的计算

上文我们已经计算得到了失配所导致的 ΔI，但通常我们所需的是失配产生的 V_OS 而不是 ΔI。为了将 ΔI 转换为输出端 V_OS，我们只需要将其乘以 R_out 即可：

$$ V_{OS}=\Delta I\times R_{out} $$

将输出端 V_OS 转换为输入端 V_OS，需要将 V_OS / Av：

$$ \begin{align} V_{OS,in}&=\frac{V_{OS,out}}{A_V} \\ &= \frac{\Delta I\times R_{out}}{G_{m}\times R_{out}} \\ &= \frac{\Delta I}{G_{m}} \\ \end{align} $$

---

整体失调的计算

将上文所述的 ΔI (β) 与 ΔI (V_TH) 整合，并等效为输入端 V_OS，可得：

$$ \begin{align} V_{OS} &= \frac{(\Delta I(\beta _{5-6,10-11})+\Delta I(V_{TH_{5-6,10-11}}))R_{Out}}{A_V} +\Delta V_{TH_{1,2}} \\ &=\frac{g_{m_{5,6}}}{g_{m_{1,2}}} \Delta V_{TH_{5,6}}+\frac{g_{m_{10,11}}}{g_{m_{1,2}}} \Delta V_{TH_{10,11}} + \frac{I_D(\frac{\Delta \beta _{1,2}}{\beta _{1,2}} +\frac{\Delta \beta _{5,6}}{\beta _{5,6}})R_{Out}}{g_{m_{1,2}}R_{Out}} +\frac{2I_D\frac{\Delta \beta _{10,11}}{\beta _{10,11}}R_{Out}}{g_{m_{1,2}}R_{Out}} + \Delta V_{TH_{1,2}} \\ &=\frac{g_{m_{5,6}}}{g_{m_{1,2}}} \Delta V_{TH_{5,6}}+\frac{g_{m_{10,11}}}{g_{m_{1,2}}} \Delta V_{TH_{10,11}} + \frac{V_{GS_1}-V_{TH_1}}{2} (\frac{\Delta \beta _{1,2}}{\beta _{1,2}} +\frac{\Delta \beta _{5,6}}{\beta _{5,6}}+2\frac{\Delta \beta _{10,11}}{\beta _{10,11}}) + \Delta V_{TH_{1,2}} \end{align} $$

---

参考阅读

差分运放失调电压的手工计算

[原创] 差分运放输入失调分析