电感型 DC-DC 电源拓扑的组成无外乎开关、电感与电容的组合变换,本文记录了常见常用的电感型 DC-DC 电源的基础拓扑结构,包括 Buck、Boost 与 Buck-Boost 三类结构的简要说明解释。
前置知识:电感的伏秒平衡
伏秒原则:处于稳定状态的电感,开关导通时间(电流上升段)的伏秒数须与开关关断(电流下降段)时的伏秒数在数值上相等,尽管两者符号相反。这也表示,绘出电感电压对时间的曲线,导通时段曲线的面积必须等于关断时段曲线的面积。用公式表示即为:
$$ V_{on}\times T_{on}=V_{off}\times T_{off} $$1、Buck(降压型)拓扑

Buck 拓扑的结构如图,SW 为功率开关,L 为功率电感,D 为功率(续流)二极管。
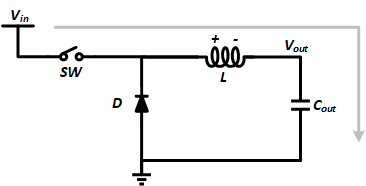
开关 SW 闭合时,电流路径如灰色箭头所示方向流动。此时,电感与输出电容被串联在电源上同时充电,电感上体现的电压极性为左正右负,二极管 D 由于反向电压的存在而处于截止状态。

开关 SW 断开时,由于电感 “来拒去留” 的特性,电感 L 会尽力维持电路中电流的恒定不会突变。因此,电感两端的电压极性被反转,给输出电容 C 以及负载进行供电。为了在 SW 断开后仍有电流回路存在,二极管 D 作为串联在回路中的续流二极管被导通。电路中电流路径如灰色箭头所示。
就这样,开关不断地开启与关闭,电感上的能量就不断地被充入与释放,达到一个动态平衡。由于充能过程中电感与输出电容处于串联状态,且放能过程中电感与输出电容处于并联状态,所以电容两端的电压永远不能超过电源电压。这就是降压型拓扑,也称为 Buck 拓扑。
我们可以通过伏秒平衡来对 Buck 电路的输出电压与占空比关系进行推导。假设一个周期内,开关开启的时长为 DT,开关关断的时长为 (1-D)T,二极管与开关均为理想器件,则有:
$$ \left\{\begin{matrix} V_{on}=V_{in}-V_{out} \\ V_{off}=V_{out} \end{matrix}\right. $$ $$ \begin{align} V_{on}\times DT&=V_{off}\times (1-D)T \\ (V_{in}-V_{out})DT&=V_{out}(1-D)T \\ V_{out}&=DV_{in}\\ \frac{V_{out}}{V_{in}} &=D \end{align} $$同时,对同步 Buck 电路还有另一种理解方法:功率开关产生的不同占空比的方波具有不同的直流分量(斩波),功率级的 L 与 C 组成了 LC 滤波网络,将不同的直流分量提取出来,得到直流分量的输出。
2、Boost(升压型)拓扑

Boost 拓扑的结构如图,SW 为功率开关,L 为功率电感,D 为功率(续流)二极管。

当开关 SW 闭合时,电源通过灰色箭头所示的电流方向为电感 L 充电,此时电感上的电压方向如图所示。
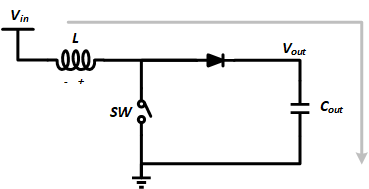
当开关 SW 断开时,由于电感上的电流不能突变,L 为了维持电流方向而翻转了自身的电压极性,体现为左负右正。此时,电源与电感呈现串联结构,共同通过续流二极管为输出电容 C 进行充电。
与 Buck 结构不同,Boost 结构仅在开关断开时为输出电容进行充电,且充电过程中相当于两个电源串联输出。因此,Boost 结构的输出电压总是大于输入电压的,为升压拓扑结构。
通过伏秒平衡来对 Boost 电路的输出电压与占空比关系进行推导。假设一个周期内,开关开启的时长为 DT,开关关断的时长为 (1-D)T,二极管与开关均为理想器件,则有:
$$ \left\{\begin{matrix} V_{on}=V_{in} \\ V_{off}=V_{out}-V_{in} \end{matrix}\right. $$ $$ \begin{align} V_{on}\times DT&=V_{off}\times (1-D)T \\ V_{in}DT&=(V_{out}-V_{in})(1-D)T \\ V_{out}&=\frac{1}{1-D} V_{in}\\ \frac{V_{out}}{V_{in}} &=\frac{1}{1-D} \end{align} $$3、Buck-Boost(升降压型)拓扑
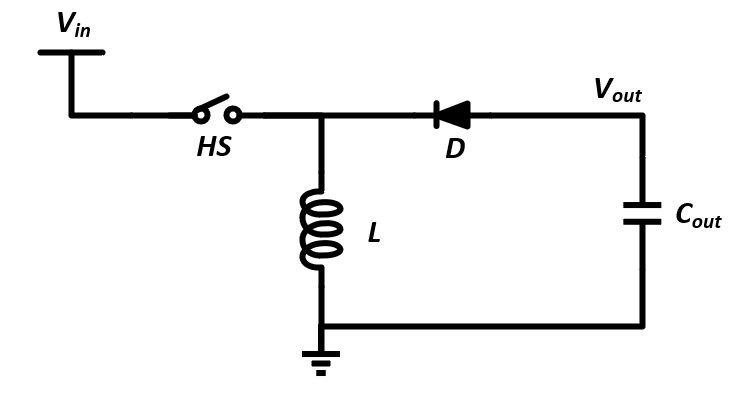
Buck-Boost 拓扑的结构如图,SW 为功率开关,L 为功率电感,D 为功率(续流)二极管。
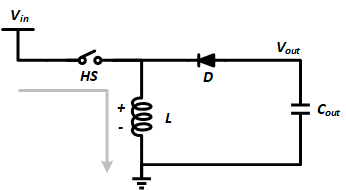
当开关 HS 闭合时,电源通过灰色箭头所示的电流方向为电感 L 充电,此时电感上的电压方向为上正下负,续流二极管 D 反相截止。
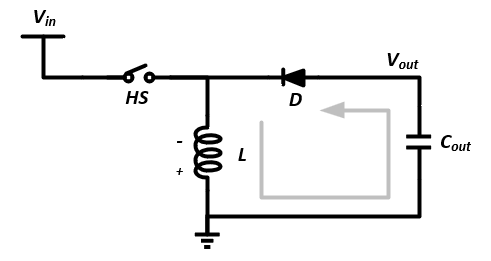
当开关 HS 断开时,由于电感电流无法突变,因此电感会反转自己的电压极性,变为上负下正。此时电流的路径通过续流二极管 D 形成,如灰色箭头所示,为输出电容 Cout 充电。
从这样的电流路径可以得出,Buck-Boost 电路的输出电压相对于地是负压。
通过伏秒平衡来对 Buck-Boost 电路的输出电压与占空比关系进行推导。假设一个周期内,开关开启的时长为 DT,开关关断的时长为 (1-D)T,二极管与开关均为理想器件,则有:
$$ \left\{\begin{matrix} V_{on}=V_{in} \\ V_{off}=-V_{out} \end{matrix}\right. $$ $$ \begin{align} V_{on}\times DT&=V_{off}\times (1-D)T \\ V_{in}DT&=-V_{out}(1-D)T \\ V_{out}&=-\frac{D}{1-D} V_{in}\\ \frac{V_{out}}{V_{in}} &=-\frac{D}{1-D} \end{align} $$为什么 Buck-Boost 可以升压?因为电感的电流无法突变,因此在开关动作时,电感两端的电压会突变。同时,这个突变电压的大小取决于电感中储存的能量大小。
所以在充入足够的能量时(D > 0.5),根据电感的电压公式:
$$ U=L\frac{di}{dt} $$电感先被缓慢充电(D 内),再被快速放电(1 – D 内),在电感两端产生的电压就会大于输入的电压,进而在电容两端产生大于 Vin 的电压,达到升压的效果。