朋友们好啊，我是什么都不会的DT。刚才有个朋友问我说DT发生什么事了，我说怎么回事，给我发了几张实验报告。我一看，嗷！原来是前几天，有两个运放实验，一个基本运算，一个非线性应用，一个有四个小实验，一个有三个小实验，他们说 …

做实验的时候云里雾里的，做完就被赶回来了，什么都不懂，什么都不会，这怎么行呢？再这样下去就成学术废物了！于是花了一些时间来对这些运放电路进行了分析。

以下电路的分析前提：在含运放电路中，当运放具有负反馈电路时，适用“虚短虚断”原则。运放工作在线性区。

---

一、反相比例运算电路

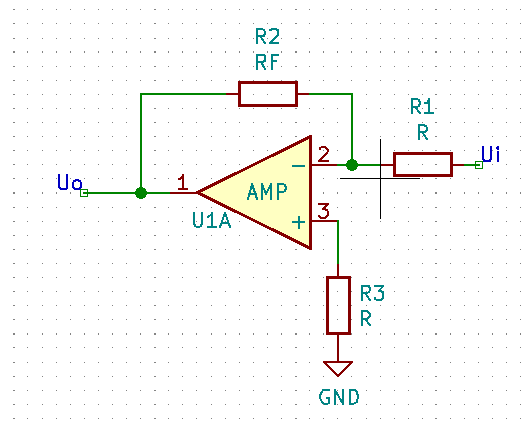
电路作用：用于输出一个与输入成负比例的电压，通常比例为$-\frac{R_{F}}{R_{1}}$

对该电路应用虚短虚断原则，有如下公式：

$$\begin{aligned} &\begin{cases} I_{N} =I_{P} \approx0 &\text{, 虚断}\\ U_{N} \approx U_{P} =R_{3} \times I_{P} =0 &\text{, 虚短}\end{cases}\\ &\Rightarrow I_{R_{1}}=I_{R_{F}} +I_{N} \approx I_{R_{F}}\\ &\Rightarrow \frac{U_{i}-U_{N}}{R_{1}} = \frac{U_{o}-U_{N}}{R_{F}}\\ &\Rightarrow U_{o} = -\frac{R_{F}}{R_{1}}\times U_{i}\end{aligned}$$

其中

$$R_{3}=R_{1}//R_{F}$$

（由于手头没有负压电源，只搭建同相电路）

---

二、同相比例运算电路

电路作用：用于输出一个与输入成正比例的电压，通常比例为$(1+\frac{R_{F}}{R_{1}})$

对该电路应用虚短虚断原则，有如下公式：

$$\begin{aligned} &\begin{cases} I_{N} =I_{P} \approx0 &\text{, 虚断}\\ U_{N} \approx U_{P} =U_{i} &\text{, 虚短} \end{cases}\end{aligned}$$

对反相输入节点使用KCL定律，有

$$\begin{aligned}&\frac{U_{i}}{R_{1}} = -\frac{U_{i}-U_{o}}{R_{F}}\\ &\Rightarrow -U_{i}\times\frac{R_{F}}{R_{1}} = U_{i}-U_{o}\\ &\Rightarrow {U_{o}} = U_{i}\times(1+\frac{R_{F}}{R_{1}})\end{aligned}$$

其中

$$R_{3}=R_{1}//R_{F}$$

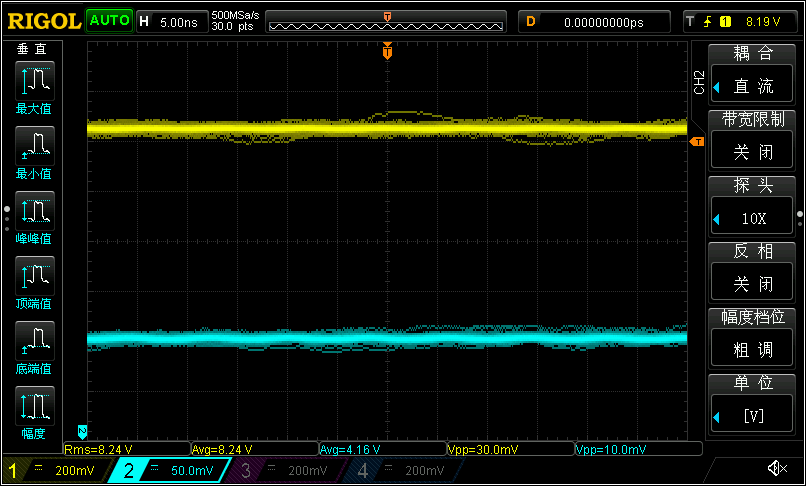
实例搭建：

运放为NE5532，Rf=R1=1KΩ，R=470Ω。

运放供电为Riden RD6006，12V/0.5A，输入电压为锂电池供电。

CH1为运放输出，CH2为电源供电。

---

三、反相求和运算电路

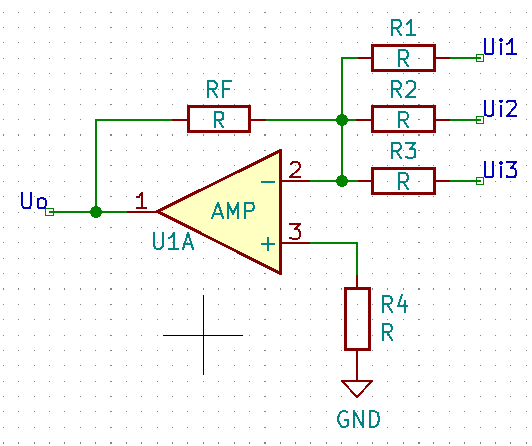
电路作用：用于输出一个与输入电压和成一负比例的电压，通常输出结果为$$-R_{F} \times (U_{i_{1}}+U_{i_{2}}+U_{i_{3}})$$

对该电路应用虚短虚断原则，有如下公式：

$$\begin{aligned} &\begin{cases} I_{N} =I_{P} \approx0 &\text{, 虚断}\\ U_{N} \approx U_{P} =R_{4} \times I_{P} =0 &\text{, 虚短}\end{cases}\end{aligned}$$

对反相输入节点使用KCL定律，有

$$\begin{aligned} &\frac{U_{i_{1}}}{R_{1}}+\frac{U_{i_{2}}}{R_{2}}+\frac{U_{i_{3}}}{R_{3}} = -\frac{U_{o}}{R_{F}}\\ &\Rightarrow U_{o} = -R_{F} \times (\frac{U_{i_{1}}}{R_{1}}+\frac{U_{i_{2}}}{R_{2}}+\frac{U_{i_{3}}}{R_{3}})\end{aligned}$$

其中

$$R_{4}=R_{1}//R_{2}//R_{3}//R_{F}$$ 。

当

$$R_{1}=R_{2}=R_{3}=R_{F}$$ 时， $$U_{o} = -R_{F} \times (U_{i_{1}}+U_{i_{2}}+U_{i_{3}})$$

---

四、同相求和运算电路

电路作用：用于输出一个与输入电压和成一正比例的电压，通常输出结果为

$$R_{F}(\frac{U_{i_{1}}}{R_{1}}+\frac{U_{i_{2}}}{R_{2}}+\frac{U_{i_{3}}}{R_{3}})$$

类比于同相比例运算电路，存在

$${U_{o}} = U_{i}\times(1+\frac{R_{F}}{R_{1}})$$

因此，对同相输入节点使用KCL定律，有

$$\begin{aligned} &\frac{U_{i_{1}}-U_{P}}{R_{1}}+\frac{U_{i_{2}}-U_{P}}{R_{2}}+\frac{U_{i_{3}}-U_{P}}{R_{3}} = \frac{U_{P}}{R_{4}}\\&\Rightarrow U_{P} = R_{P} \times (\frac{U_{i_{1}}}{R_{1}}+\frac{U_{i_{2}}}{R_{2}}+\frac{U_{i_{3}}}{R_{3}})\end{aligned}$$

，其中

$$R_{P}=R_{1}//R_{2}//R_{3}//R_{4}$$ .

由上可得：

$$U_{o}=\frac{R_{P}}{R_{N}}\times R_{F}(\frac{U_{i_{1}}}{R_{1}}+\frac{U_{i_{2}}}{R_{2}}+\frac{U_{i_{3}}}{R_{3}})$$ ，其中 $$R_{N}=R_{5}//R_{F}$$

若使

$$R_{N}=R_{P}$$ ，可得 $$U_{o}=R_{F}(\frac{U_{i_{1}}}{R_{1}}+\frac{U_{i_{2}}}{R_{2}}+\frac{U_{i_{3}}}{R_{3}})$$

---

符号说明：I_N – 反相输入端电流；
I_P – 同相输入端电流；
U_N – 反相输入端电压；
U_P – 同相输入端电压；
I_Rn – Rn上的电流；
U_Rn – Rn上的电压；
R₁ // R₂ … // R_n – R₁、R₂到R_n并联

使用绘图软件：KiCad